MathType - The #Gradient descent is an iterative optimization #algorithm for finding local minimums of multivariate functions. At each step, the algorithm moves in the inverse direction of the gradient, consequently reducing
Por um escritor misterioso
Last updated 22 dezembro 2024

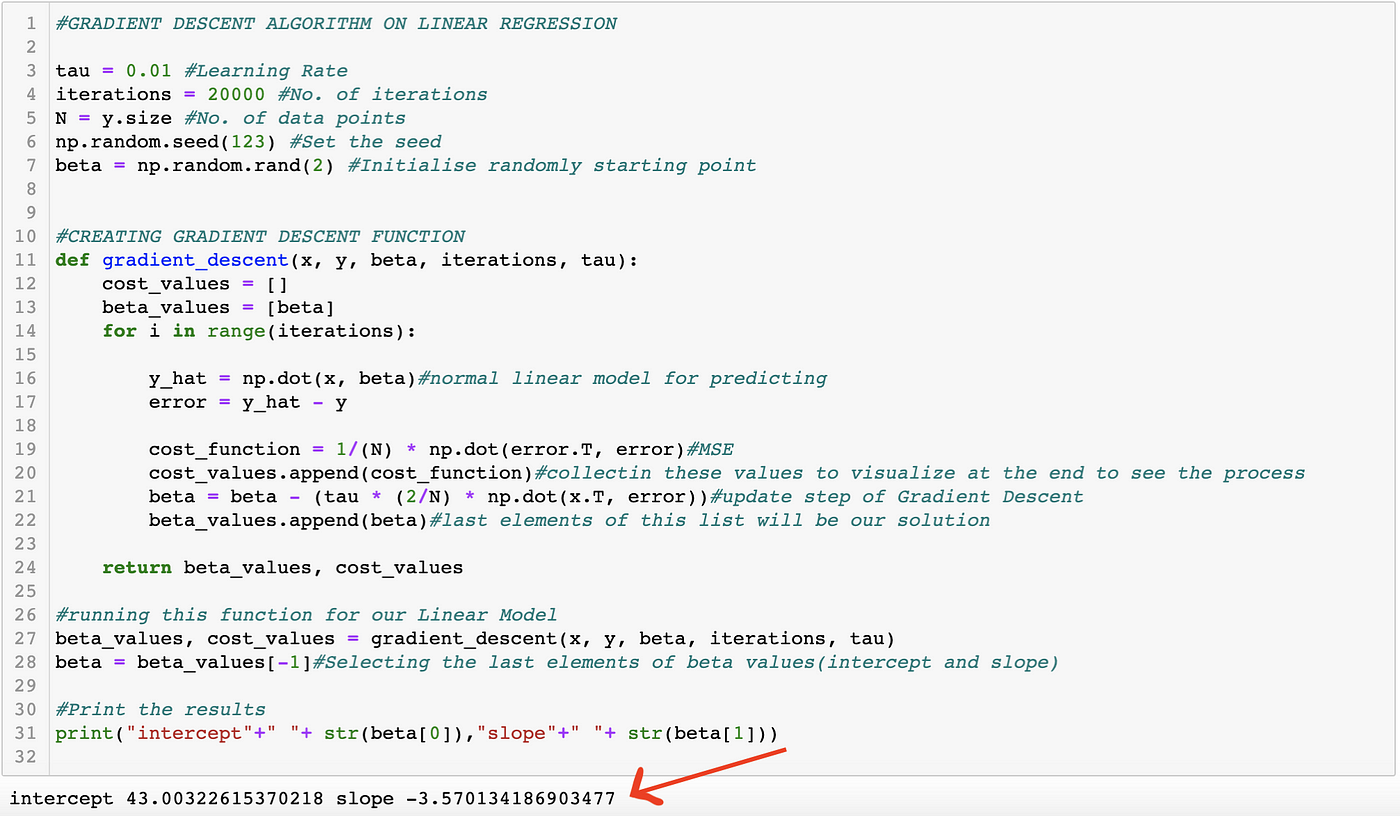
Explanation of Gradient Descent Optimization Algorithm on Linear Regression example., by Joshgun Guliyev, Analytics Vidhya
All About Gradient Descent. Gradient descent is an optimization…, by Md Nazrul Islam
How to figure out which direction to go along the gradient in order to reach local minima in gradient descent algorithm - Quora

Optimization Techniques used in Classical Machine Learning ft: Gradient Descent, by Manoj Hegde

Solved Exercise 1 (7points) 1a. Explain the idea of gradient

2.1.2 Gradient Descent for Multiple Variables by Andrew Ng
Solved] . 4. Gradient descent is a first—order iterative optimisation
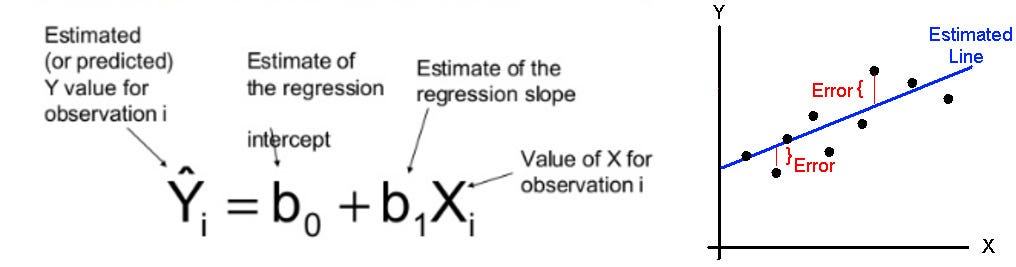
Gradient Descent algorithm. How to find the minimum of a function…, by Raghunath D
Can gradient descent be used to find minima and maxima of functions? If not, then why not? - Quora
All About Gradient Descent. Gradient descent is an optimization…, by Md Nazrul Islam

MathType - The #Gradient descent is an iterative optimization #algorithm for finding local minimums of multivariate functions. At each step, the algorithm moves in the inverse direction of the gradient, consequently reducing

Gradient descent is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. To find a local minimum of a function using gradient descent, we take steps proportional
Recomendado para você
-
Method of steepest descent - Wikipedia22 dezembro 2024
-
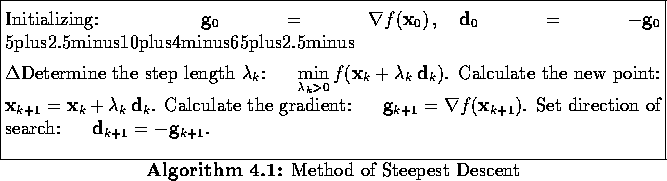 Method of Steepest Descent22 dezembro 2024
Method of Steepest Descent22 dezembro 2024 -
 PPT - 4. Method of Steepest Descent PowerPoint Presentation, free download - ID:565484522 dezembro 2024
PPT - 4. Method of Steepest Descent PowerPoint Presentation, free download - ID:565484522 dezembro 2024 -
 Descent method — Steepest descent and conjugate gradient in Python, by Sophia Yang, Ph.D.22 dezembro 2024
Descent method — Steepest descent and conjugate gradient in Python, by Sophia Yang, Ph.D.22 dezembro 2024 -
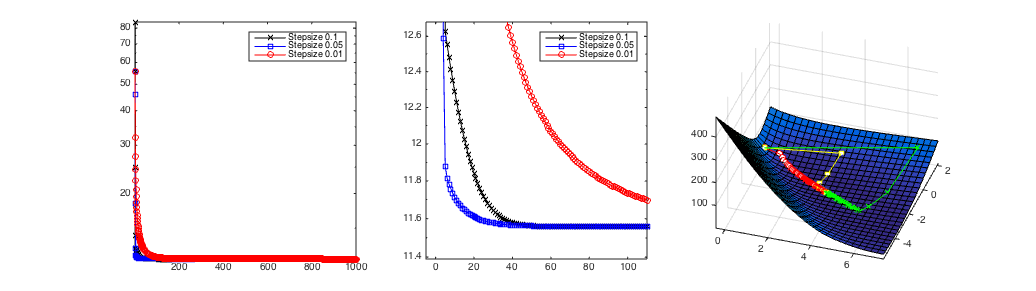 Lecture 8: Gradient Descent (and Beyond)22 dezembro 2024
Lecture 8: Gradient Descent (and Beyond)22 dezembro 2024 -
 Guide to gradient descent algorithms22 dezembro 2024
Guide to gradient descent algorithms22 dezembro 2024 -
 The A-Z Guide to Gradient Descent Algorithm and Its Types22 dezembro 2024
The A-Z Guide to Gradient Descent Algorithm and Its Types22 dezembro 2024 -
 The Steepest-Descent Method - ppt download22 dezembro 2024
The Steepest-Descent Method - ppt download22 dezembro 2024 -
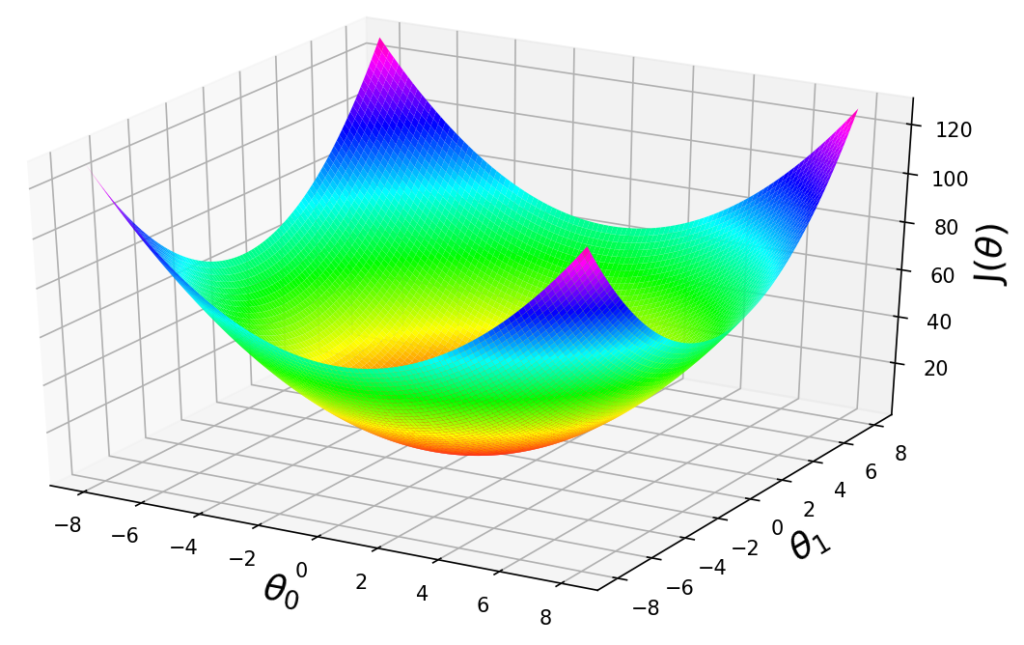 Guide to Gradient Descent Algorithm: A Comprehensive implementation in Python - Machine Learning Space22 dezembro 2024
Guide to Gradient Descent Algorithm: A Comprehensive implementation in Python - Machine Learning Space22 dezembro 2024 -
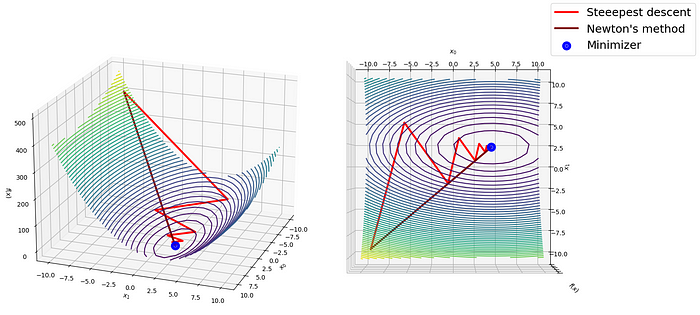 Steepest Descent and Newton's Method in Python, from Scratch: A… – Towards AI22 dezembro 2024
Steepest Descent and Newton's Method in Python, from Scratch: A… – Towards AI22 dezembro 2024
você pode gostar
-
 Steam Community :: Among Us VR22 dezembro 2024
Steam Community :: Among Us VR22 dezembro 2024 -
 Create a Todas as temporadas de one piece Tier List - TierMaker22 dezembro 2024
Create a Todas as temporadas de one piece Tier List - TierMaker22 dezembro 2024 -
 Calaméo - Guia Completo Seo Quarta Edicao22 dezembro 2024
Calaméo - Guia Completo Seo Quarta Edicao22 dezembro 2024 -
 The implementation procedure of Deep Conviction Systems (DCS) for22 dezembro 2024
The implementation procedure of Deep Conviction Systems (DCS) for22 dezembro 2024 -
/i.s3.glbimg.com/v1/AUTH_da025474c0c44edd99332dddb09cabe8/internal_photos/bs/2023/X/g/Tq1hjeRTu2AncPDFz4nw/captura-de-tela-2023-04-20-as-17.10.33.png) Brennand é Francisco e não existe outro': filha do artista22 dezembro 2024
Brennand é Francisco e não existe outro': filha do artista22 dezembro 2024 -
 Mangá Savanna Game - 2ª temporada - Mangás JBC22 dezembro 2024
Mangá Savanna Game - 2ª temporada - Mangás JBC22 dezembro 2024 -
BORUTO: NARUTO NEXT GENERATIONS Escape - Watch on Crunchyroll22 dezembro 2024
-
 How to Draw an Easy Face, Step by Step, Faces, People, FREE Online Drawing Tutorial, Added by Dawn, September 25,…22 dezembro 2024
How to Draw an Easy Face, Step by Step, Faces, People, FREE Online Drawing Tutorial, Added by Dawn, September 25,…22 dezembro 2024 -
 Transport Then and Now - Memory Game22 dezembro 2024
Transport Then and Now - Memory Game22 dezembro 2024 -
 World Championship 2011 Card Pack : YuGiOh Card Prices22 dezembro 2024
World Championship 2011 Card Pack : YuGiOh Card Prices22 dezembro 2024
